В стране 100 городов, некоторые пары городов соединены дорогой с односторонним движением. Известно, что из любого города можно доехать до любого другого, но при закрытии любой дороги это условие нарушается. Какое наибольшее число дорог может быть в этой стране? (Любые два города соединены не более чем одной дорогой.)
Подсказка
Попробуйте доказать лемму. Если в связном ориентированном графе 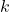 вершин и хотя бы
вершин и хотя бы 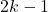 ребро (причем некоторые пары вершин могут быть соединены ребрами в обоих направлениях), то одно из ребер можно удалить без потери связности.
ребро (причем некоторые пары вершин могут быть соединены ребрами в обоих направлениях), то одно из ребер можно удалить без потери связности.
Решение
Ответ. 197.
Решение: Построим ориентированный граф, вершины которого соответствуют городам, а ребра — дорогам (направление ребра будет соответствовать направлению дороги). Любые две вершины соединены не более, чем одним ориентированным ребром. Полученный граф будет связным (из любой вершины можно попасть в любую другую), но при удалении любого ребра связность теряется.
Построим пример такого графа со 197 ребрами. Он будет состоять из вершин 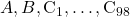 , и ребер
, и ребер 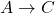 , а также
, а также 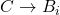 и
и 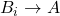 для всех
для всех 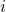 . Нетрудно проверить, что этот граф подходит.
. Нетрудно проверить, что этот граф подходит.
Докажем лемму: если в связном ориентированном графе 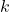 вершин и хотя бы
вершин и хотя бы 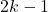 ребро (причем некоторые пары вершин могут быть соединены ребрами в обоих направлениях), то одно из ребер можно удалить без потери связности.
ребро (причем некоторые пары вершин могут быть соединены ребрами в обоих направлениях), то одно из ребер можно удалить без потери связности.
Доказательство: Рассмотрим в нашем графе произвольную вершину  . Нетрудно понять, что достаточно отметить в графе
. Нетрудно понять, что достаточно отметить в графе 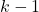 ребро, чтобы только по отмеченным вершинам можно было бы добраться из
ребро, чтобы только по отмеченным вершинам можно было бы добраться из  до любой другой вершины. Аналогично, можно отметить в графе еще
до любой другой вершины. Аналогично, можно отметить в графе еще 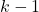 ребро так, чтобы по отмеченным вершинам можно было бы добраться из любой другой вершины до
ребро так, чтобы по отмеченным вершинам можно было бы добраться из любой другой вершины до  . В графе должны остаться неотмеченные ребра — любое из них можно удалить без потери связности. Лемма доказана.
. В графе должны остаться неотмеченные ребра — любое из них можно удалить без потери связности. Лемма доказана.
Перейдем к доказательству утверждения задачи. Из связности графа следует, что в нем есть (ориентированный) цикл  . Понятно, что
. Понятно, что  и нет никаких ребер между входящими в цикл вершинами, кроме ребер самого цикла (иначе такое ребро можно удалить без потери связности). Также отметим, что из любой не входящей в цикл вершины А существует не более одного ребра, выходящего к вершинам цикла (если таких ребер хотя бы два, то одно из них можно удалить без потери связности). Аналогично, существует не более одного ребра, выходящего из вершин цикла в А.
и нет никаких ребер между входящими в цикл вершинами, кроме ребер самого цикла (иначе такое ребро можно удалить без потери связности). Также отметим, что из любой не входящей в цикл вершины А существует не более одного ребра, выходящего к вершинам цикла (если таких ребер хотя бы два, то одно из них можно удалить без потери связности). Аналогично, существует не более одного ребра, выходящего из вершин цикла в А.
Заменим все вершины цикла на одну вершину 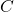 и для любой другой вершины
и для любой другой вершины  проведем ребро
проведем ребро 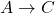 , если существует одно из ребер
, если существует одно из ребер 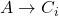 и ребро
и ребро 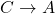 , если существует одно из ребер
, если существует одно из ребер 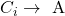 . Получится новый связный ориентированный графG’, в котором ровно на
. Получится новый связный ориентированный графG’, в котором ровно на 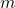 ребер меньше, чем в исходном графе и удаление любого ребра нарушает связность. (Однако, в этом графе возможно наличие двух ребер разного направления между двумя вершинами.) В графе G’ ровно
ребер меньше, чем в исходном графе и удаление любого ребра нарушает связность. (Однако, в этом графе возможно наличие двух ребер разного направления между двумя вершинами.) В графе G’ ровно 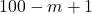 вершина и, по доказанному выше утверждению, не более
вершина и, по доказанному выше утверждению, не более 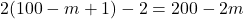 ребер. Следовательно, в исходном графе было не более, чем
ребер. Следовательно, в исходном графе было не более, чем 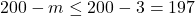 ребер.
ребер.
![]() и
и ![]() , а максимальный размер пустого подграфа —
, а максимальный размер пустого подграфа — ![]() . Тогда есть такие множества вершин
. Тогда есть такие множества вершин ![]() и
и ![]() мощности
мощности ![]() каждое, что
каждое, что ![]() и
и ![]() соответственно являются в них единственными ребрами. Выкинем из графа все вершины, кроме
соответственно являются в них единственными ребрами. Выкинем из графа все вершины, кроме ![]() , от этого условие не изменится. После этого все вершины множества
, от этого условие не изменится. После этого все вершины множества ![]() , кроме вершины
, кроме вершины ![]() , ни с какой вершиной не соединены. Поэтому их тоже можно выбросить, после чего как
, ни с какой вершиной не соединены. Поэтому их тоже можно выбросить, после чего как ![]() , так и количества элементов в
, так и количества элементов в ![]() и
и ![]() уменьшатся на одну и ту же величину. После этого у нас остался граф на
уменьшатся на одну и ту же величину. После этого у нас остался граф на ![]() вершине; если в нем нет нечетного цикла, то он двудольный, тогда в нем есть пустой подграф на
вершине; если в нем нет нечетного цикла, то он двудольный, тогда в нем есть пустой подграф на ![]() вершине, что не так. Следовательно, нечетный цикл есть.
вершине, что не так. Следовательно, нечетный цикл есть.