Ориентированные графы — Страница 2 — Задачи на Графы

Задача 079

01.01.2025 от

В компании из 100 человек некоторые знакомы друг с другом. Каждую минуту из компании уходит человек, который имеет знакомых больше, чем любой из оставшихся. Через несколько минут такого человека не нашлось. Какое наименьшее количество людей могло остаться к этому моменту в компании?

Подсказка

Предположим, что могло остаться не более двух человек. Рассмотрим момент, когда осталось ровно три человека $A, B, C$ .

Решение

Ответ: 3.

Решение. Оценка. Предположим, что могло остаться не более двух человек. Рассмотрим момент, когда осталось ровно три человека $A, B, C$ . Пусть $A$ тот, у кого больше всех знакомых. Если у $A$ один знакомый, то у кого-то из $B$ и $C$ тоже есть один знакомый (сам $A$ ), но тогда у $A$ не больше всех знакомых. Следовательно, у $A$ два знакомых и он знаком с $B$ и $C$ . Пусть $D$ — человек, который ушел перед $A$ . Так как у $A$ хотя бы два знакомых из $B, C$ и $D$ , то у $D$ их должно быть не менее 3 . Значит, $D$ знаком с $A, B$ и $C$ . Но тогда и у $A$ три знакомых. Противоречие.

Пример. Выстроим людей в ряд и познакомим каждого со всеми, кроме его соседей в ряду. Кроме того, не будем знакомить 1 и 3 человек в ряду. Последний человек в ряду знаком со всеми, кроме одного (если людей больше трех). А все остальные люди в ряду имеют как минимум двух незнакомых. Более того, после ухода последнего получается ряд, вновь удовлетворяющий условиям выше. Следовательно, люди будут уходить, пока не останется 3 человека.

Задача 086

01.01.2025 от

В виртуальном компьютерном государстве не менее двух городов. Некоторые пары городов соединены дорогой, причём из каждого города можно добраться по дорогам до любого другого (здесь и далее переходить с дороги на дорогу разрешается только в городах). Если при этом можно, начав движение из какого-то города и не проходя дважды по одной и той же дороге, вернуться в этот город, государство называется сложным, иначе — простым. Петя и Вася играют в такую игру. В начале игры Петя указывает на каждой дороге направление, в котором по ней можно двигаться, и помещает в один из городов туриста. Далее за ход Петя перемещает туриста по дороге в разрешённом направлении в соседний город, а Вася в ответ меняет направление одной из дорог, входящей или выходящей из города, куда попал турист. Вася победит, если в какой-то момент Петя не сможет сделать ход. Докажите, что
а) в простом государстве Петя может играть так, чтобы не проиграть, как бы ни играл Вася;
б) в сложном государстве Вася может гарантировать себе победу, как бы ни играл Петя.

Подсказка

a) Условие означает, что граф — дерево. Петя выбирает произвольную вершину. От каждой вершины существует ровно один путь в выбранную. Все рёбра на этом пути он ориентирует в сторону выбранной вершины.

б) По условию граф связен и содержит цикл. Будем доказывать индукцией по количеству вершин, что Вася может гарантировать себе победу, причём для любой изначальной расстановки стрелок перед его ходом (включая «невозможный» случай, когда все стрелки ведут из вершины, где стоит фишка перед первым ходом Васи).

Решение

Рассмотрим граф, вершинами которого являются города, а рёбрами — дороги.
a) Условие означает, что граф — дерево. Петя выбирает произвольную вершину. От каждой вершины существует ровно один путь в выбранную. Все рёбра на этом пути он ориентирует в сторону выбранной вершины.

Первым ходом Петя перемещает туриста в выбранную вершину. Все ориентированные пути ведут к туристу. Вася разворачивает одно ребро. Турист идёт по нему. Ясно, что все пути снова ведут к нему. Вася снова разворачивает одно ребро и так далее. Поэтому у Пети всегда есть ход и он не проиграет.
б) По условию граф связен и содержит цикл. Будем доказывать индукцией по количеству вершин, что Вася может гарантировать себе победу, причём для любой изначальной расстановки стрелок перед его ходом (включая «невозможный» случай, когда все стрелки ведут из вершины, где стоит фишка перед первым ходом Васи).

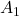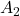База — простые циклы. Пусть в простом цикле $A_{1} A_{2} \ldots A_{n}$ как-то расставлены стрелки на рёбрах и турист смог сделать ход, пойдя из $A_{1}$ в $A_{2}$ . Вася будет разворачивать стрелки перед ним. Поэтому турист не сможет идти в обратную сторону. Допустим, турист смог дойти до 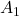$A_{1}$ . Тогда перед ним разворачивают стрелку, и ему некуда идти. Петя проиграл.

Шаг индукции. Граф не является простым циклом. Выберем в нём цикл С минимальной длины. Ясно, что 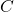$C$ — простой и не содержит ребёр внутри себя. Поэтому есть вершины вне 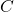$C$ . Выберем из них вершину 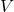$V$ с максимальным расстоянием до 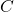$C$ . Обозначим граф без 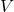$V$ буквой 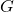$G$ . Ясно, что 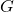$G$ связен и содержит цикл.

По предположению индукции в 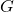$G$ есть выигрышная стратегия для Васи при любой ориентации рёбер. Внутри 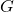$G$ Вася будет следовать ей. Так как в 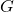$G$ Петя проигрывает, то турист вынужден будет когда-то пойти в 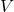$V$ . Тогда Вася развернёт эту стрелку. Турист выйдет из 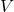$V$ , а Вася сделает любой допустимый ход в 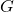$G$ . Турист пойдёт внутри 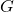$G$ . Сейчас у Васи опять есть выигрышная стратегия в 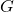$G$ , которой он и будет следовать. Турист снова будет вынужден зайти в 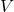$V$ , уменьшив количество стрелок, идущих из 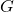$G$ в $V$ . 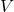В конце концов они кончатся, и Петя проиграет в 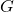$G$ , если он не проиграл раньше.

Задача 096

01.01.2025 от

На полке в беспорядке стоит 100 -томная энциклопедия, один из томов которой — в красном переплете. Красный том можно поменять местами с любым другим. Какого наименьшего количества таких обменов заведомо хватит, чтобы расставить тома по порядку?

Подсказка

Построим ориентированный граф, вершинами которого будут числа от 1 до 100 , а каждое из ребер связывает номер места, на котором стоит том с данным номером, с самим этим номером. Поскольку из каждой вершины этого графа выходит ровно одно ребро, и в каждую его вершину входит ровно одно ребро, все его вершины и ребра разбиваются на непересекающиеся ориентированные циклы.

Решение

Ответ: 148.

Решение. Пример на 148. Построим ориентированный граф, вершинами которого будут числа от 1 до 100 , а каждое из ребер связывает номер места, на котором стоит том с данным номером, с самим этим номером. Поскольку из каждой вершины этого графа выходит ровно одно ребро, и в каждую его вершину входит ровно одно ребро, все его вершины и ребра разбиваются на непересекающиеся ориентированные циклы. Цикл, в который входит красный том, назовем особым, прочие — обычными. Возьмем любой обычный цикл $a \rightarrow b \rightarrow c \rightarrow \ldots \rightarrow d \rightarrow a$ и добавим в него красный том (пусть его номер равен $r$ ): $a \rightarrow r \rightarrow b \rightarrow c \rightarrow \ldots \rightarrow d \rightarrow a$ . Затем последовательно поменяем местами красный том со всеми остальными элементами получившегося цикла. В итоге все элементы исходного обычного цикла встанут на предписанные им места, а красный том вернется на исходное место. Проделаем описанную процедуру со всеми обычными циклами длины, не меньшей 2 , а напоследок «прокрутим» особый цикл, после чего все тома окажутся на своих местах, т.е. будут идти в порядке возрастания. При этом на приведение в порядок каждого цикла длины $n$ , кроме особого, у нас ушла $n+1$ перестановка, а на особый цикл — $n-1$ перестановка, а всего — $100+k-2$ перестановки, где $k$ — число циклов длины не меньше 2 . Поскольку циклов длины 2 и больше не более 50, мы совершили не больше 148 перестановок. Оценка. Пусть получилось 50 циклов длины 2. На приведение в порядок каждого обычного цикла нужно минимум 3 перестановки: убрать один том, поставить на его место другой и поставить на место другого первый. Еще одна перестановка нужна на особый цикл. Итого $49 \times 3+1=148$ .

Задача 099

01.01.2025 от

Дан связный граф на 2009 вершинах. Докажите, что в нем можно выделить 2008 ребер и расставить на них стрелки так, чтобы для любых двух вершин, соединенных ребром в исходном графе, из одной из них в другую можно было бы пройти по стрелкам.

Подсказка

Отметим в нашем графе $G$ любую вершину $a$ и построим дерево поиска в глубину $T$ с корнем $a$ .

Решение

Отметим в нашем графе $G$ любую вершину $a$ и построим дерево поиска в глубину $T$ с корнем $a$ .

Пронумеруем вершину $a$ числом 0 и будем добавлять в дерево и нумеровать вершины по следующему принципу: если в дереве есть вершины с номерами от 1 до $k$ , то рассмотрим вершину с наибольшим номером, из которой выходит хотя бы одно ребро в вершину, не принадлежащую уже построенному дереву, добавим любое из таких рёбер в дерево, и новой вершине присвоим номер $k+1$ . Все ребра дерева $T$ ориентируем от меньшего номера к большему.

Пусть $t(x)$ — номер вершины $x$ при построении дерева $T$ . Докажем, что все требования задачи выполняются. Очевидно, в остовном дереве графа на 2009 вершинах как раз 2008 ребер, так что мы поставили 2008 стрелочек. Пусть $u v$ — ребро исходного графа $G$ , причем $t(u)<t(v)$ . Если $u v$ входит в $T$ , всё в порядке. В противном случае вершина $v$ подвешена в $T$ к вершине $v_{1} \neq u$ . Так как в графе $G$ вершина $v$ смежна с $u$ , то по построению дерева $t\left(v_{1}\right)>t(u)$ , и $t(v)>t\left(v_{1}\right)$ . Рассмотрим момент, когда добавлялась вершина $v_{1}$ . Так как в этот момент в дереве еще нет смежной с $u$ вершины $v$ , то по построению вершина $v_{1}$ подвешена в $T$ к вершине $v_{2}$ , где $t\left(v_{1}\right)>t\left(v_{2}\right) \geq t(u)$ . И так далее, пока очередная вершина $v_{m}$ не окажется совпадающей с $u$ (это случится, потому что номера $t\left(v_{i}\right)$ монотонно убывают, и все они не меньше, чем $t(u)$ ). Искомый путь $u=v_{m} \rightarrow v_{m-1} \rightarrow \ldots \rightarrow v_{1} \rightarrow v$ построен.