В классе поровну мальчиков и девочек, и все ученики разного роста. Оказалось, что если мальчик дружит с девочкой, то он дружит и со всеми девочками выше неё; и наоборот — если девочка дружит с мальчиком, то она дружит и со всеми мальчиками выше него. Учитель физкультуры хочет выстроить детей в ряд, начиная с мальчика, так, чтобы любые двое соседей в ряду были друзьями разного пола. Оказалось, что количество способов это сделать — натуральное число 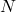 , делящееся на 101. Каким наименьшим количеством нулей может оканчиваться десятичная запись числа
, делящееся на 101. Каким наименьшим количеством нулей может оканчиваться десятичная запись числа 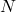 ?
?
Подсказка
Для начала докажите лемму.
Лемма. 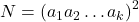 , где
, где 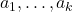 — некоторая последовательность неотрицательных целых чисел такая, что
— некоторая последовательность неотрицательных целых чисел такая, что 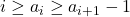 при всех
при всех  .
.
Решение
Ответ. 48.
Решение: Назовём исследуемые расстановки легальными. Пусть 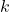 количество мальчиков. Пример получается при
количество мальчиков. Пример получается при 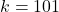 , когда все дружат. Действительно, тогда
, когда все дружат. Действительно, тогда 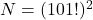 , причём 2 входит в 101 ! хотя бы в 50 степени, а 5 — в степени
, причём 2 входит в 101 ! хотя бы в 50 степени, а 5 — в степени ![Rendered by QuickLaTeX.com [101 / 5]+\left[101 / 5^{2}\right]=24](https://mathgraphs.ru/wp-content/ql-cache/quicklatex.com-7993675eb0588ee12e3865f38ee77614_l3.png) , ибо
, ибо 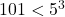 . Значит,
. Значит, 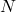 оканчивается ровно 48 нулями.
оканчивается ровно 48 нулями.
Лемма. 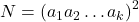 , где
, где 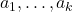 — некоторая последовательность неотрицательных целых чисел такая, что
— некоторая последовательность неотрицательных целых чисел такая, что 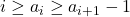 при всех
при всех  .
.
Сначала выведем оценку из леммы. Поскольку 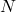 натурально,
натурально,  , то есть
, то есть 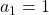 . Если
. Если 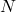 делится на 101 , то одно из чисел
делится на 101 , то одно из чисел 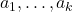 делится на
делится на 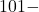 скажем, это
скажем, это 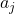 . Из условий
. Из условий 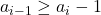 следует, что среди чисел
следует, что среди чисел 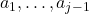 встретятся все числа от 1 до 100 , то есть
встретятся все числа от 1 до 100 , то есть 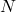 делится на (
делится на ( 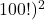 и, следовательно, на
и, следовательно, на 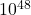 .
.
Осталось доказать лемму. Числа 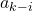 будут определяться так. Выкинем из компании
будут определяться так. Выкинем из компании 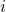 самых маленьких девочек и
самых маленьких девочек и 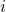 самых больших мальчиков. Тогда
самых больших мальчиков. Тогда 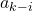 — это количество оставшихся мальчиков, знакомых со всеми оставшимися девочками. Из этого описания немедленно следуют условия на
— это количество оставшихся мальчиков, знакомых со всеми оставшимися девочками. Из этого описания немедленно следуют условия на 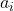 , указанные в лемме.
, указанные в лемме.
Индукция по 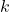 . При
. При 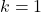 имеем
имеем 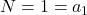 . Пусть теперь
. Пусть теперь 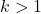 . Рассмотрим самую маленькую девочку
. Рассмотрим самую маленькую девочку 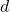 ; пусть
; пусть 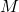 — множество мальчиков, которые с ней дружат,
— множество мальчиков, которые с ней дружат, 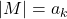 . Заметим, что
. Заметим, что 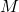 состоит из
состоит из 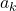 самых высоких мальчиков.
самых высоких мальчиков.
В любой легальной расстановке перед 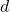 стоит мальчик
стоит мальчик 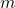 из
из 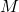 , а после неё — либо мальчик
, а после неё — либо мальчик 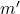 из
из 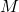 , либо никто. Так как
, либо никто. Так как 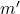 , если он существует, знаком со всеми девочками, то после выбрасывания пары (
, если он существует, знаком со всеми девочками, то после выбрасывания пары ( 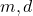 ) из расстановки получится легальная расстановка оставшихся детей. Наоборот, в любую легальную расстановку
) из расстановки получится легальная расстановка оставшихся детей. Наоборот, в любую легальную расстановку 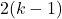 детей, отличных от
детей, отличных от 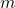 и
и 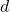 , пару (
, пару ( 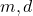 ) можно вставить либо перед произвольным
) можно вставить либо перед произвольным 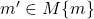 , либо в конец, то есть
, либо в конец, то есть 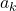 способами.
способами.
Далее, поскольку 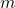 дружит со всеми, для всех
дружит со всеми, для всех 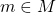 после выкидывания пары (
после выкидывания пары ( 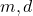 ) останутся «одинаковые» компании детей (научным языком, графы их дружб изоморфны). Поэтому в них будет поровну легальных расстановок, и эти количества будут по предположению индукции иметь вид
) останутся «одинаковые» компании детей (научным языком, графы их дружб изоморфны). Поэтому в них будет поровну легальных расстановок, и эти количества будут по предположению индукции иметь вид 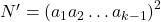 . Итак, для каждого из
. Итак, для каждого из 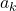 мальчиков из
мальчиков из 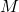 в каждую из
в каждую из 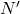 перестановок можно вставить пару (
перестановок можно вставить пару ( 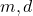 ) ровно
) ровно 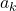 способами. Значит,
способами. Значит, 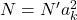 , что и требовалось.
, что и требовалось.
![]() , из которого можно попасть в наибольшее число городов. Если есть город
, из которого можно попасть в наибольшее число городов. Если есть город ![]() , в который нельзя попасть из
, в который нельзя попасть из ![]() , то из
, то из ![]() можно попасть в
можно попасть в ![]() , а, значит, и во все города, в которые можно попасть из
, а, значит, и во все города, в которые можно попасть из ![]() . Получается противоречие: из
. Получается противоречие: из ![]() можно попасть в большее число городов, чем из
можно попасть в большее число городов, чем из ![]() . Значит из города
. Значит из города ![]() можно попасть во все города.
можно попасть во все города.