Дано натуральное число п. Назовём словом последовательность из 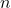 нулей и единиц, а маской — последовательность из п нулей, единии, и звёздочек. Слово соответствует маске, если оно получено из неё заменой звёздочек на нули и единицы. Рассмотрим набор масок
нулей и единиц, а маской — последовательность из п нулей, единии, и звёздочек. Слово соответствует маске, если оно получено из неё заменой звёздочек на нули и единицы. Рассмотрим набор масок 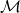 , удовлетворяющий следующим двум условиям:
, удовлетворяющий следующим двум условиям:
(1) каждое слово соответствует ровно одной маске, и
(2) для каждой из п позиций найдётся маска из 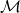 , в которой в этой позиции стоит не звездочка.
, в которой в этой позиции стоит не звездочка.
Найдите наименьшее возможное количество масок в таком наборе 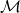 .
.
Подсказка
Рассмотрим двудольный граф 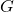 , в котором вершинами одной из долей будут номера позиций в слове длины
, в котором вершинами одной из долей будут номера позиций в слове длины 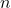 , вершинами второй из долей будут маски, а рёбрами соединим каждую маску с теми позициями, на которых стоит не звездочка. Пусть доля
, вершинами второй из долей будут маски, а рёбрами соединим каждую маску с теми позициями, на которых стоит не звездочка. Пусть доля  это вершины
это вершины  , соответствующие номерам позиций, а доля
, соответствующие номерам позиций, а доля  это вершины
это вершины 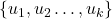 , соответствующие маскам.
, соответствующие маскам.
Решение
Рассмотрим двудольный граф 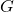 , в котором вершинами одной из долей будут номера позиций в слове длины
, в котором вершинами одной из долей будут номера позиций в слове длины 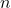 , вершинами второй из долей будут маски, а рёбрами соединим каждую маску с теми позициями, на которых стоит не звездочка. Пусть доля
, вершинами второй из долей будут маски, а рёбрами соединим каждую маску с теми позициями, на которых стоит не звездочка. Пусть доля  это вершины
это вершины  , соответствующие номерам позиций, а доля
, соответствующие номерам позиций, а доля  это вершины
это вершины 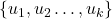 , соответствующие маскам.
, соответствующие маскам.
Докажем, что в графе 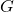 для доли
для доли  выполнено условие леммы Холла. Предположим противное. Рассмотрим в
выполнено условие леммы Холла. Предположим противное. Рассмотрим в  минимальное по включению множество
минимальное по включению множество  , для которого условие леммы Холла не выполнено. То есть у вершин из
, для которого условие леммы Холла не выполнено. То есть у вершин из  количество соседей меньше, чем
количество соседей меньше, чем 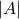 , а для любого подмножества
, а для любого подмножества 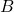 множества
множества  количество соседей у вершин из
количество соседей у вершин из 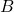 хотя бы
хотя бы 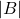 . Отсюда следует, что у
. Отсюда следует, что у  ровно
ровно  соседних вершин. Без ограничения общности будем считать, что
соседних вершин. Без ограничения общности будем считать, что  , а
, а 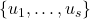 это соседние вершины множества
это соседние вершины множества  . Тогда для множества
. Тогда для множества 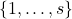 выполнена лемма Холла. Пусть без ограничения общности существует паросочетание
выполнена лемма Холла. Пусть без ограничения общности существует паросочетание 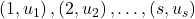 . Значит, в словах
. Значит, в словах 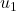 ,
, 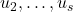 на
на 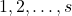 местах соответственно стоят не звёздочки (пусть без ограничения общности там стоят нули). Рассмотрим маски
местах соответственно стоят не звёздочки (пусть без ограничения общности там стоят нули). Рассмотрим маски 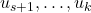 . По построению в этих масках на местах с 1 по
. По построению в этих масках на местах с 1 по  стоят звёздочки. Так как каждое слово можно получить из масок ровно одним способом, то из масок
стоят звёздочки. Так как каждое слово можно получить из масок ровно одним способом, то из масок 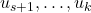 получаются не все слова. Значит, существует множество слов
получаются не все слова. Значит, существует множество слов 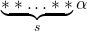 (на первых
(на первых  позициях стоит что угодно, а затем идёт слово
позициях стоит что угодно, а затем идёт слово 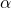 длины
длины  ), которое нельзя получить из масок
), которое нельзя получить из масок 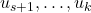 . Тогда слово
. Тогда слово 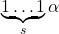 нельзя получить ни из какой маски. Противоречие.
нельзя получить ни из какой маски. Противоречие.
Следовательно, для доли  выполнено условие леммы Холла. Рассмотрим любое паросочетание, покрывающее долю
выполнено условие леммы Холла. Рассмотрим любое паросочетание, покрывающее долю  . Пусть это паросочетание
. Пусть это паросочетание  , а в словах
, а в словах 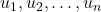 на
на  местах соответственно стоят нули. Тогда чтобы получить слово
местах соответственно стоят нули. Тогда чтобы получить слово 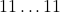 нам нужна ещё хотя бы одна маска. Откуда и получаем оценку на
нам нужна ещё хотя бы одна маска. Откуда и получаем оценку на 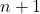 .
.
![]() — наш граф,
— наш граф, ![]() — множество всех остовных деревьев графа
— множество всех остовных деревьев графа ![]() , а М(
, а М( ![]() ) — множество всех остовных подграфов графа
) — множество всех остовных подграфов графа ![]() , имеющих ровно один цикл. Рассмотрим произвольное дерево
, имеющих ровно один цикл. Рассмотрим произвольное дерево ![]() . В нем нечетное число ребер, следовательно, количество не вошедших в
. В нем нечетное число ребер, следовательно, количество не вошедших в ![]() ребер графа
ребер графа ![]() также нечетно. Если к дереву
также нечетно. Если к дереву ![]() добавить любое не вошедшее в него ребро графа
добавить любое не вошедшее в него ребро графа ![]() , то получится граф из
, то получится граф из ![]() . Всего таким образом из дерева
. Всего таким образом из дерева ![]() получается нечетное число графов из
получается нечетное число графов из ![]() . Наоборот, рассмотрим любой граф
. Наоборот, рассмотрим любой граф ![]() и его единственный цикл
и его единственный цикл ![]() . Граф
. Граф ![]() может быть получен добавлением ребра к тем деревьям, которые получаются из
может быть получен добавлением ребра к тем деревьям, которые получаются из ![]() удалением одного из ребер цикла
удалением одного из ребер цикла ![]() . Так как граф
. Так как граф ![]() двудольный, то в цикле
двудольный, то в цикле ![]() — четное число ребер, следовательно, у графа
— четное число ребер, следовательно, у графа ![]() — четное число остовных деревьев-«»предков»». Отсюда следует, что в множестве
— четное число остовных деревьев-«»предков»». Отсюда следует, что в множестве ![]() четное число остовных деревьев.
четное число остовных деревьев.