Степени всех вершин графа 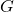 меньше
меньше 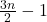 (где
(где 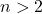 ), причем среди любых
), причем среди любых 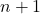 вершин есть две несмежных. Назовем блоком множество из
вершин есть две несмежных. Назовем блоком множество из 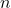 попарно смежных вершин графа
попарно смежных вершин графа 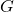 . Известно, что любые два блока имеют общую вершину. Докажите, что все блоки имеют общую вершину.
. Известно, что любые два блока имеют общую вершину. Докажите, что все блоки имеют общую вершину.
Подсказка
Лемма 1. (В.Л. Дольников). В графе 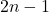 вершин. Оказалось, что после выкидывания любой вершины графа найдется полный подграф с
вершин. Оказалось, что после выкидывания любой вершины графа найдется полный подграф с 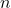 вершинами. Тогда в исходном графе найдется полный подграф с
вершинами. Тогда в исходном графе найдется полный подграф с 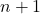 вершиной.
вершиной.
Лемма 2. Пусть 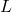 — пересечение нескольких блоков графа
— пересечение нескольких блоков графа 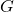 , причем
, причем 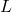 непусто. Тогда
непусто. Тогда 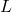 содержит не менее
содержит не менее 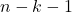 вершин.
вершин.
Решение
Лемма 1. (В.Л. Дольников). В графе 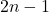 вершин. Оказалось, что после выкидывания любой вершины графа найдется полный подграф с
вершин. Оказалось, что после выкидывания любой вершины графа найдется полный подграф с 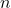 вершинами. Тогда в исходном графе найдется полный подграф с
вершинами. Тогда в исходном графе найдется полный подграф с 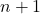 вершиной.
вершиной.
Доказательство. Пусть утверждение леммы неверно. Будем считать 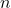 наименьшим натуральным числом, для которого существует граф, не удовлетворяющий условию задачи. Рассмотрим граф
наименьшим натуральным числом, для которого существует граф, не удовлетворяющий условию задачи. Рассмотрим граф 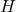 , дополнительный к графу из условия. Рассмотрим любой пустой подграф графа
, дополнительный к графу из условия. Рассмотрим любой пустой подграф графа  с
с 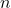 вершинами, множество его вершин обозначим через
вершинами, множество его вершин обозначим через 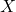 , а множество остальных вершин через
, а множество остальных вершин через 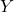 . Назовем подмножество
. Назовем подмножество 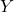 плохим, если количество вершин в нем больше количества вершин в
плохим, если количество вершин в нем больше количества вершин в 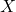 , смежных хотя бы с одной вершиной из этого подмножества. Обозначим через
, смежных хотя бы с одной вершиной из этого подмножества. Обозначим через 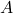 максимальное плохое подмножество (оно может быть и пустым), пусть оно содержит
максимальное плохое подмножество (оно может быть и пустым), пусть оно содержит 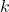 вершин, тогда в
вершин, тогда в 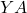 нет плохих подмножеств, поэтому, в силу леммы Холла, каждой вершине
нет плохих подмножеств, поэтому, в силу леммы Холла, каждой вершине 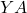 можно сопоставить смежную с ней вершину
можно сопоставить смежную с ней вершину 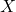 таким образом, чтобы все эти вершины были различны и не смежны с вершинами из Y
таким образом, чтобы все эти вершины были различны и не смежны с вершинами из Y  A. Множество не сопоставленных вершин
A. Множество не сопоставленных вершин 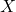 обозначим через
обозначим через 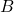 . Рассмотрим граф
. Рассмотрим граф 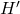 , образованный вершинами
, образованный вершинами 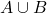 и ребрами графа
и ребрами графа 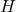 , соединяющими эти вершины. Заметим, что при выкидывании любой вершины
, соединяющими эти вершины. Заметим, что при выкидывании любой вершины 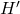 в графе
в графе 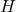 должен был найтись пустой подграф с
должен был найтись пустой подграф с 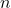 вершинами, но в него могло входить не более, чем
вершинами, но в него могло входить не более, чем 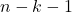 вершина из (
вершина из ( 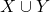 )
)  , следовательно, остальные
, следовательно, остальные 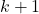 вершин должны быть из
вершин должны быть из 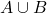 , поэтому в
, поэтому в 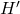 после выкидывания любой вершины найдется пустой подграф с
после выкидывания любой вершины найдется пустой подграф с 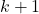 вершинами, но тогда, в силу минимальности
вершинами, но тогда, в силу минимальности 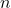 либо в
либо в 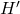 найдется пустой подграф с
найдется пустой подграф с 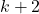 вершинами, либо
вершинами, либо  . В первом случае, добавляя к вершинам этого подграфа вершины из
. В первом случае, добавляя к вершинам этого подграфа вершины из 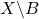 , получим пустой подграф с
, получим пустой подграф с 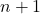 вершинами, во втором — выкинем вершину из
вершинами, во втором — выкинем вершину из 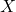 , несмежную ни с одной вершиной
, несмежную ни с одной вершиной 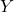 , найдем пустой подграф
, найдем пустой подграф 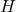 с
с 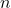 вершинами и добавим к нему эту вершину, получим пустой подграф
вершинами и добавим к нему эту вершину, получим пустой подграф 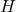 с
с 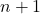 вершинами. Полученное противоречие доказывает утверждение леммы.
вершинами. Полученное противоречие доказывает утверждение леммы.
Обозначим через 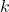 разность максимальной степени графа и
разность максимальной степени графа и 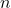 . Из условия следует, что
. Из условия следует, что 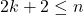 .
.
Лемма 2. Пусть 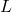 — пересечение нескольких блоков графа
— пересечение нескольких блоков графа 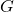 , причем
, причем 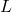 непусто. Тогда
непусто. Тогда 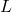 содержит не менее
содержит не менее 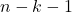 вершин.
вершин.
Доказательство. Пусть 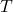 — объединение всех блоков, содержащих
— объединение всех блоков, содержащих 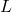 . Тогда
. Тогда 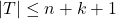 , поскольку любая вершина из
, поскольку любая вершина из 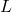 смежна с любой вершиной из
смежна с любой вершиной из 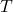 . Ясно, что любой блок, содержащий
. Ясно, что любой блок, содержащий 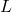 , имеет не менее
, имеет не менее 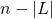 вершин в
вершин в 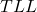 . Пусть
. Пусть 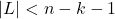 . Заметим, что при выкидывании любой вершины из
. Заметим, что при выкидывании любой вершины из 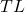 найдется блок, содержащий
найдется блок, содержащий 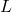 , но не содержащий выкинутой вершины (поскольку
, но не содержащий выкинутой вершины (поскольку 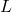 — пересечение всех блоков, содержащих
— пересечение всех блоков, содержащих 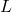 ). Но в
). Но в 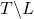 нет подграфов, содержащих более
нет подграфов, содержащих более 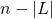 вершин (иначе объединение такого подграфа с
вершин (иначе объединение такого подграфа с 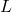 будет полным подграфом графа
будет полным подграфом графа 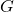 , содержащим более
, содержащим более 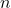 вершин). Тогда
вершин). Тогда 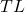 содержит не менее
содержит не менее  вершин в силу леммы 1 . Следовательно,
вершин в силу леммы 1 . Следовательно,  , откуда
, откуда 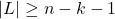 . Лемма доказана.
. Лемма доказана.
Завершение доказательства. Рассмотрим любой блок. Назовем его Н. Рассмотрим пересечение всех блоков, имеющих непустое пересечение с 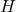 (включая
(включая 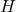 ). Будем добавлять эти блоки по одному и следить за пересечением. До тех пор, пока оно непусто, оно содержит не менее
). Будем добавлять эти блоки по одному и следить за пересечением. До тех пор, пока оно непусто, оно содержит не менее 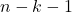 вершин, в силу леммы 2 . Но тогда следующий добавляемый подграф должен иметь не менее
вершин, в силу леммы 2 . Но тогда следующий добавляемый подграф должен иметь не менее 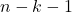 общих вершин с
общих вершин с 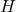 (в силу леммы 2 ), но
(в силу леммы 2 ), но 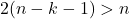 (по условию
(по условию 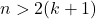 ), следовательно новый блок имеет непустое пересечение с пересечением старых.
), следовательно новый блок имеет непустое пересечение с пересечением старых.
![]() из 8 девочек найдётся (возможно, пустое) подмножество
из 8 девочек найдётся (возможно, пустое) подмножество ![]() такое, что любой мальчик, знакомый со всеми девочками из
такое, что любой мальчик, знакомый со всеми девочками из ![]() , знаком ещё хотя бы с одной девочкой из
, знаком ещё хотя бы с одной девочкой из ![]() . Докажите, что в любом множестве
. Докажите, что в любом множестве ![]() из 300 мальчиков найдётся (возможно, пустое) подмножество
из 300 мальчиков найдётся (возможно, пустое) подмножество ![]() такое, что любая девочка, знакомая со всеми мальчиками из
такое, что любая девочка, знакомая со всеми мальчиками из ![]() , знакома ещё хотя бы с одним мальчиком из
, знакома ещё хотя бы с одним мальчиком из ![]() .
.![]() может быть взято за
может быть взято за ![]() тогда и только тогда, когда ни для какого мальчика множество его знакомых в
тогда и только тогда, когда ни для какого мальчика множество его знакомых в ![]() не совпадает с
не совпадает с ![]() . Аналогично с
. Аналогично с ![]() и
и ![]() .
.![]() может быть взято за
может быть взято за ![]() тогда и только тогда, когда ни для какого мальчика множество его знакомых в
тогда и только тогда, когда ни для какого мальчика множество его знакомых в ![]() не совпадает с
не совпадает с ![]() . Аналогично с
. Аналогично с ![]() и
и ![]() . Предположим, что нашлось множество из
. Предположим, что нашлось множество из ![]() мальчиков, в котором нельзя выделить
мальчиков, в котором нельзя выделить ![]() , удовлетворяющее условию. Тогда для любого
, удовлетворяющее условию. Тогда для любого ![]() найдется девочка, которая в множестве
найдется девочка, которая в множестве ![]() знакома в точности с мальчиками из
знакома в точности с мальчиками из ![]() . Выберем в
. Выберем в ![]() мальчиков, из них — 256 , и каждому мальчику сопоставим своё четырёхзначное двоичное число. Выберем 8 девочек так, чтобы
мальчиков, из них — 256 , и каждому мальчику сопоставим своё четырёхзначное двоичное число. Выберем 8 девочек так, чтобы ![]() -ая девочка знала в множестве
-ая девочка знала в множестве ![]() в точности тех мальчиков, которым сопоставлено число с 1 в
в точности тех мальчиков, которым сопоставлено число с 1 в ![]() -ом разряде (мальчиков, которым ничего не сопоставлено, все эти девочки не знают). Тогда легко видеть, что в выбранном множестве девочек никакое подмножество нельзя назначить
-ом разряде (мальчиков, которым ничего не сопоставлено, все эти девочки не знают). Тогда легко видеть, что в выбранном множестве девочек никакое подмножество нельзя назначить ![]() . Действительно, если
. Действительно, если ![]() — номера девочек в подмножестве, то мальчик, которому сопоставлено число с единицами в разрядах
— номера девочек в подмножестве, то мальчик, которому сопоставлено число с единицами в разрядах ![]() и нулями во всех остальных разрядах, из восьми выбранных девочек знает в точности
и нулями во всех остальных разрядах, из восьми выбранных девочек знает в точности ![]() .
.