B стране 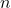 городов, один из которых является столицей. Между некоторыми парами городов налажено авиасообщение. Расстоянием между городами называется минимальное количество перелетов, которые необходимо совершить, чтобы добраться от одного города до другого. Правительство хочет закрыть авиасообщение между некоторыми парами городов, чтобы расстояние от столицы до любого другого города не изменилось. Известно, что существует нечетное количество способов, которыми правительство может это сделать. В том числе, считается способ, в котором не закрывается ничего.
городов, один из которых является столицей. Между некоторыми парами городов налажено авиасообщение. Расстоянием между городами называется минимальное количество перелетов, которые необходимо совершить, чтобы добраться от одного города до другого. Правительство хочет закрыть авиасообщение между некоторыми парами городов, чтобы расстояние от столицы до любого другого города не изменилось. Известно, что существует нечетное количество способов, которыми правительство может это сделать. В том числе, считается способ, в котором не закрывается ничего.
Докажите, что нельзя, стартовав в некотором городе и совершив нечетное число перелетов, вернуться обратно в него.
Подсказка
Для каждой вершины посчитаем расстояние от неё до столицы. Очевидно, что для двух вершин, соединенных ребром, эти расстояния отличаются не более чем на 1. Предположим, что в графе нашелся нечетный цикл. Пройдем по этому циклу и будем следить за изменением расстояния при переходе по каждому ребру.
Решение
Рассмотрим граф, в котором вершины — города, ребра — наличие сообщения. Для каждой вершины посчитаем расстояние от неё до столицы. Очевидно, что для двух вершин, соединенных ребром, эти расстояния отличаются не более чем на 1. Предположим, что в графе нашелся нечетный цикл. Пройдем по этому циклу и будем следить за изменением расстояния при переходе по каждому ребру. Так как цикл нечетный, то если каждый раз расстояние менялось ровно на 1 , то придя в исходную вершину мы бы получили расстояние другой четности, чего быть не может. Следовательно, хотя бы один раз при проходе по ребру цикла расстояние не изменилось. То есть существует ребро  , что оба конца этого ребра находятся на одинаковом расстоянии от столицы.
, что оба конца этого ребра находятся на одинаковом расстоянии от столицы.
Назовем набор ребер хорошим, если при удалении из графа всех ребер, кроме ребер этого набора, расстояние до столицы не изменятся. Докажем, что хорошие наборы можно разбить на пары следующим образом: если в наборе есть  , то уберем
, то уберем  из набора, а если нет
из набора, а если нет  , то добавим. То есть надо доказать, что если мы удалили несколько рёбер и расстояния не изменились, то при удалении/добавлении ребра
, то добавим. То есть надо доказать, что если мы удалили несколько рёбер и расстояния не изменились, то при удалении/добавлении ребра  расстояния также не изменятся. Про добавление ребра
расстояния также не изменятся. Про добавление ребра  утверждение очевидно, так как от добавления ребра расстояния не могут уменьшиться, а увеличиться не могут, так как они равны расстояниям в графе, в котором никакие ребра не удалены. Предположим, что при удалении
утверждение очевидно, так как от добавления ребра расстояния не могут уменьшиться, а увеличиться не могут, так как они равны расстояниям в графе, в котором никакие ребра не удалены. Предположим, что при удалении  расстояние от какого-то города
расстояние от какого-то города 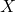 до столицы
до столицы 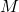 увеличилось. Тогда кратчайший путь от
увеличилось. Тогда кратчайший путь от 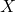 до
до 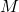 проходил через
проходил через  . Но такого не может быть, ведь расстояния от концов
. Но такого не может быть, ведь расстояния от концов  до
до 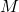 одинаковы, и мы могли, не проходя по ребру
одинаковы, и мы могли, не проходя по ребру  , добраться от
, добраться от 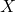 до
до 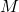 за меньшее число шагов.
за меньшее число шагов.
Таким образом, все наборы разбились на пары, то есть их четное число. Противоречие.