Город Сугробск представляет собой квадрат со стороной 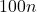 метров, разбитый прямыми улицами на
метров, разбитый прямыми улицами на 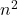 одинаковых кварталов (
одинаковых кварталов ( 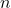 — чётное натуральное число, большее 2). На каждой из
— чётное натуральное число, большее 2). На каждой из 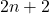 улиц, идущих по сторонам кварталов от края до края города, введено одностороннее движение. На соседних параллельных улицах движение направлено в разные стороны. В одном из углов города находится автопарк; обе выходящие из этого угла улицы направлены от автопарка. Снегоуборочная машина выезжает из автопарка и начинает убирать снег. Чтобы не портить дорожное покрытие, по уже убранным участкам (кроме перекрестков) машина не ездит. В конце смены машина должна прибыть в противоположный угол города. Какое наибольшее расстояние она может проехать?
улиц, идущих по сторонам кварталов от края до края города, введено одностороннее движение. На соседних параллельных улицах движение направлено в разные стороны. В одном из углов города находится автопарк; обе выходящие из этого угла улицы направлены от автопарка. Снегоуборочная машина выезжает из автопарка и начинает убирать снег. Чтобы не портить дорожное покрытие, по уже убранным участкам (кроме перекрестков) машина не ездит. В конце смены машина должна прибыть в противоположный угол города. Какое наибольшее расстояние она может проехать?
Подсказка
Докажите, что наименьшее количество не пройденных отрезков есть 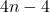 .
.
Решение
Ответ. 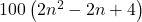 .
.
Решение: Будем считать, что машина едет из левого нижнего в правый верхний угол, а все стороны маленьких квадратов равны 1 . Всего горизонтальных единичных отрезков 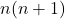 , тогда всего единичных отрезков
, тогда всего единичных отрезков 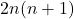 . Докажем, что наименьшее количество не пройденных отрезков есть
. Докажем, что наименьшее количество не пройденных отрезков есть 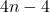 . Тогда наибольшее количество пройденных отрезков не более
. Тогда наибольшее количество пройденных отрезков не более 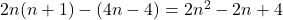 . Введем прямоугольную систему координат: левый нижний угол будет иметь координату
. Введем прямоугольную систему координат: левый нижний угол будет иметь координату 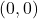 , а верхний правый — (
, а верхний правый — ( 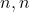 ). Рассмотрим прямые вида
). Рассмотрим прямые вида 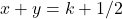 , где
, где 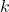 целое число от 0 до
целое число от 0 до 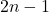 . Очевидно, что ее пересекает поровну вертикальных и горизонтальных отрезков, ввиду симметрии относительно
. Очевидно, что ее пересекает поровну вертикальных и горизонтальных отрезков, ввиду симметрии относительно 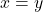 . Так как начальная и конечная точка нашего маршрута находятся по разные стороны от этой прямой, то маршрут пересечет ее нечетное число раз, а, следовательно, один из отрезков будет не пройденным. Итого уже не пройденных отрезков будет 2n. Рассмотрим прямую
. Так как начальная и конечная точка нашего маршрута находятся по разные стороны от этой прямой, то маршрут пересечет ее нечетное число раз, а, следовательно, один из отрезков будет не пройденным. Итого уже не пройденных отрезков будет 2n. Рассмотрим прямую 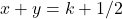 где
где 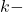 четное дислот че ниных отрезка, пескащих ра сли ренлу. По условию, если аетно, то оба дин ных отрезка ориентированы из ооласти старта в ооласть финиша, а если
четное дислот че ниных отрезка, пескащих ра сли ренлу. По условию, если аетно, то оба дин ных отрезка ориентированы из ооласти старта в ооласть финиша, а если  — нечетно, то наооорот. Всего отрезков первого типа
— нечетно, то наооорот. Всего отрезков первого типа 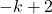 , а отрезков второго типа
, а отрезков второго типа 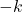 . Заметим, что пройденных отрезков первого типа должно быть ровно на один больше, чем пройденных отрезков второго типа. Однако, точки
. Заметим, что пройденных отрезков первого типа должно быть ровно на один больше, чем пройденных отрезков второго типа. Однако, точки 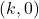 и
и 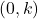 лежат на границе, поэтому в них входит ровно один отрезок, следовательно, для каждой этой точки, один из выходящих отрезков будет не пройденным. Остается не более
лежат на границе, поэтому в них входит ровно один отрезок, следовательно, для каждой этой точки, один из выходящих отрезков будет не пройденным. Остается не более 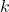 отрезков первого типа, и не более
отрезков первого типа, и не более 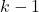 отрезков второго типа. Т.е. эта прямая пересекает хотя бы три не пройденных отрезка. Таких прямых
отрезков второго типа. Т.е. эта прямая пересекает хотя бы три не пройденных отрезка. Таких прямых 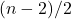 , и они дают еще
, и они дают еще  не пройденных отрезков. Аналогично, рассматривая прямую
не пройденных отрезков. Аналогично, рассматривая прямую 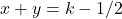 , где
, где 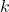 — четное число от
— четное число от 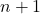 до
до 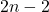 , найдем еще
, найдем еще  не пройденных отрезков. Всего не пройденных отрезков будет хотя бы
не пройденных отрезков. Всего не пройденных отрезков будет хотя бы 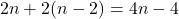 . Оценка доказана.
. Оценка доказана.
Приведем пример. Удалим все ребра вида ( 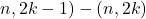 при
при 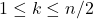 и вида (
и вида ( 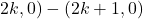 при
при 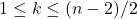 . Всего удалено
. Всего удалено  ребро. Далее удалим пути (
ребро. Далее удалим пути ( 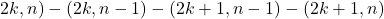 при
при 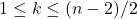 , а также пути
, а также пути 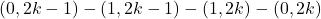 при
при 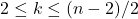 . Итого в этих путях
. Итого в этих путях 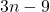 ребер. Наконец, удалим пути
ребер. Наконец, удалим пути 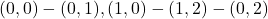 и
и 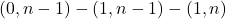 . Всего удалено
. Всего удалено 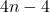 ребра. Все не граничные вершины имели степень входяших и исходяших ребер ровно по два, поэтому после удаления они остались равными. Легко проверить, что у всех вершин, лежащих строго на стороне квалрата стапо по одному входнему и исхолящему ребру У начальной и конечной вершины стало по одному исходящему и одному входящему ребру. Пример построен.
ребра. Все не граничные вершины имели степень входяших и исходяших ребер ровно по два, поэтому после удаления они остались равными. Легко проверить, что у всех вершин, лежащих строго на стороне квалрата стапо по одному входнему и исхолящему ребру У начальной и конечной вершины стало по одному исходящему и одному входящему ребру. Пример построен.
![]() команд, каждые две из которых сыграли друг с другом ровно один раз. Оказалось, что для каждых двух команд есть ровно
команд, каждые две из которых сыграли друг с другом ровно один раз. Оказалось, что для каждых двух команд есть ровно ![]() команд, у которых они обе выиграли. Докажите, что
команд, у которых они обе выиграли. Докажите, что ![]() .
.![]() . Пусть она выиграла у
. Пусть она выиграла у ![]() команд. Тогда каждая из этих
команд. Тогда каждая из этих ![]() команд выиграла ровно у
команд выиграла ровно у ![]() из этих
из этих ![]() команд — иначе нарушится условие задачи относительно нее и команды
команд — иначе нарушится условие задачи относительно нее и команды ![]() .
.![]() . Пусть она выиграла у
. Пусть она выиграла у ![]() команд. Тогда каждая из этих
команд. Тогда каждая из этих ![]() команд выиграла ровно у
команд выиграла ровно у ![]() из этих
из этих ![]() команд — иначе нарушится условие задачи относительно нее и команды
команд — иначе нарушится условие задачи относительно нее и команды ![]() . Общее число матчей в микротурнире между данными
. Общее число матчей в микротурнире между данными ![]() командами равно
командами равно ![]() с одной стороны и общему числу побед, равному
с одной стороны и общему числу побед, равному ![]() — с другой, откуда
— с другой, откуда ![]() . Осталось заметить, что в всем турнире было сыграно
. Осталось заметить, что в всем турнире было сыграно ![]() матчей и одержано
матчей и одержано ![]() побед. Значит,
побед. Значит, ![]() , откуда
, откуда ![]() .
.