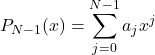К графикам функций ![]() и
и ![]() провели касательные в некоторой точке их пересечения. Докажите, что эти касательные перпендикулярны друг другу для любого
провели касательные в некоторой точке их пересечения. Докажите, что эти касательные перпендикулярны друг другу для любого ![]() .
.
РешениеРешение
Абсцисса ![]() любой точки пересечения графиков данных функций удовлетворяет равенству
любой точки пересечения графиков данных функций удовлетворяет равенству ![]() . В этой точке касательная к графику функции
. В этой точке касательная к графику функции ![]() имеет угловой коэффициент
имеет угловой коэффициент ![]() , а касательная к графику функции
, а касательная к графику функции ![]() имеет угловой коэффициент
имеет угловой коэффициент ![]() . Поскольку
. Поскольку ![]() , эти касательные перпендикулярны друг другу.
, эти касательные перпендикулярны друг другу.