Некоторые из 2017 городов страны соединены прямыми двусторонними авиарейсами так, что из каждого города можно добраться до любого другого. Правительство хочет объявить 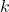 городов стратегически значимыми так, чтобы из любого города (включая стратегически значимые), совершив ровно один перелет, можно было попасть в стратегически значимый город. При каком наименьшем
городов стратегически значимыми так, чтобы из любого города (включая стратегически значимые), совершив ровно один перелет, можно было попасть в стратегически значимый город. При каком наименьшем 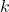 это наверняка можно будет сделать?
это наверняка можно будет сделать?
Подсказка
Очевидно, достаточно разобрать случай, когда граф — дерево (в произвольном связном графе можно выделить дерево, содержащее все его вершины; если 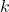 стратегически значимых вершин будет достаточно для этого дерева, их будет достаточно и для исходного графа).
стратегически значимых вершин будет достаточно для этого дерева, их будет достаточно и для исходного графа).
Докажем, что в графе с 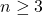 вершинами можно указать несколько вершин и выделить из них несколько стратегически значимых так, что каждая выделенная вершина будет смежна с выделенной стратегически значимой, доля стратегически значимых среди выделенных будет не больше
вершинами можно указать несколько вершин и выделить из них несколько стратегически значимых так, что каждая выделенная вершина будет смежна с выделенной стратегически значимой, доля стратегически значимых среди выделенных будет не больше 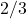 и после удаления выделенных вершин граф останется связным.
и после удаления выделенных вершин граф останется связным.
Рассмотрим две вершины 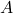 и
и 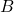 , путь между которыми содержит наибольшее количество рёбер.
, путь между которыми содержит наибольшее количество рёбер.
Решение
Ответ. При 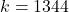 . Решение. Введём граф городов и авиарейсов. Для начала приведём пример графа, в котором меньше чем 1344 стратегически значимыми вершинами не обойтись. Пусть в графе имеются вершины
. Решение. Введём граф городов и авиарейсов. Для начала приведём пример графа, в котором меньше чем 1344 стратегически значимыми вершинами не обойтись. Пусть в графе имеются вершины 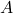 , а также
, а также 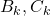 и
и 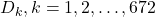 ; для каждого
; для каждого 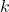 проведём рёбра между вершиной
проведём рёбра между вершиной 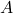 и
и 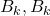 и
и 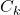 ,
, 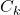 и
и 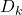 . Легко видеть, что этот граф связен. Поскольку вершина
. Легко видеть, что этот граф связен. Поскольку вершина 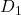 связана только с вершиной
связана только с вершиной 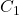 , то вершина
, то вершина 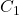 должна быть объявлена стратегически значимой. Кроме того, применяя условие задачи для вершины
должна быть объявлена стратегически значимой. Кроме того, применяя условие задачи для вершины 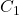 получаем, что либо вершина
получаем, что либо вершина 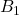 , либо вершина
, либо вершина 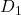 должна быть объявлена стратегически значимой. Итак, из вершин
должна быть объявлена стратегически значимой. Итак, из вершин 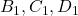 хотя бы две вершины должны быть стратегически значимыми. Рассуждая аналогично для каждой тройки
хотя бы две вершины должны быть стратегически значимыми. Рассуждая аналогично для каждой тройки 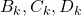 , получаем требуемое.
, получаем требуемое.
Докажем теперь, что 1344 стратегически значимыми вершинами можно обойтись. Очевидно, достаточно разобрать случай, когда граф — дерево (в произвольном связном графе можно выделить дерево, содержащее все его вершины; если 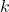 стратегически значимых вершин будет достаточно для этого дерева, их будет достаточно и для исходного графа).
стратегически значимых вершин будет достаточно для этого дерева, их будет достаточно и для исходного графа).
Докажем, что в графе с 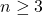 вершинами можно указать несколько вершин и выделить из них несколько стратегически значимых так, что каждая выделенная вершина будет смежна с выделенной стратегически значимой, доля стратегически значимых среди выделенных будет не больше
вершинами можно указать несколько вершин и выделить из них несколько стратегически значимых так, что каждая выделенная вершина будет смежна с выделенной стратегически значимой, доля стратегически значимых среди выделенных будет не больше 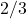 и после удаления выделенных вершин граф останется связным.
и после удаления выделенных вершин граф останется связным.
Рассмотрим две вершины 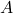 и
и 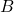 , путь между которыми содержит наибольшее количество рёбер. Пусть
, путь между которыми содержит наибольшее количество рёбер. Пусть 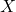 — последняя перед
— последняя перед 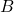 вершина на пути из
вершина на пути из 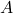 в
в 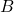 . Очевидно,
. Очевидно, 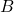 соединена только с
соединена только с 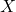 . Если
. Если 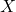 соединена с какимито висячими вершинами, кроме
соединена с какимито висячими вершинами, кроме 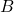 , выделим
, выделим 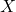 и все смежные с ней висячие вершины, а стратегически значимыми среди них объявим
и все смежные с ней висячие вершины, а стратегически значимыми среди них объявим 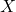 и
и 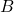 . Очевидно, удаление этих вершин не нарушит связности графа, и стратегически значимые составляют среди них не более
. Очевидно, удаление этих вершин не нарушит связности графа, и стратегически значимые составляют среди них не более 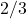 .
.
Пусть 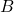 — единственная висячая вершина, соединённая с
— единственная висячая вершина, соединённая с 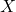 . Рассмотрим последнюю вершину
. Рассмотрим последнюю вершину 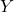 на пути из
на пути из 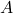 в
в 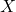 . Если все отличные от
. Если все отличные от 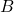 вершины, путь из которых в
вершины, путь из которых в 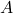 проходит через
проходит через 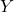 , смежны с
, смежны с 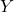 , можно выделить эти вершины,
, можно выделить эти вершины, 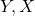 и
и 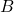 , а стратегическими среди них объявить
, а стратегическими среди них объявить 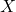 и
и 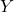 .
.
Наконец, разберём случай, когда путь из 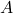 в
в 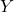 можно продолжить несколькими путями
можно продолжить несколькими путями 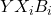 длины 2 (путями большей длины продолжить не удастся в силу максимальности выбранного выше пути из
длины 2 (путями большей длины продолжить не удастся в силу максимальности выбранного выше пути из 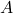 в
в 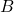 ). Пусть таких путей
). Пусть таких путей 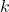 . Тогда нужно выделить все вершины этих путей и все висячие вершины, смежные с
. Тогда нужно выделить все вершины этих путей и все висячие вершины, смежные с 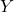 , а стратегически значимыми объявить
, а стратегически значимыми объявить 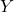 и все
и все 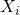 . При этом из графа будет удалено не менее
. При этом из графа будет удалено не менее 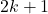 вершин, из которых
вершин, из которых 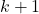 стратегически значимых, а
стратегически значимых, а 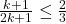 .
.
Будем продолжать эту деятельность, пока от графа не останется огрызок, содержащий не более двух вершин. Если вершин не осталось вообще, то мы объявили стратегически значимыми не более ![Rendered by QuickLaTeX.com [2 \cdot 2017 / 3]=1344](https://mathgraphs.ru/wp-content/ql-cache/quicklatex.com-efa73edcf2edc6bd28c098b1586756a7_l3.png) вершин, и процесс завершился. Если осталась одна вершина, то на предыдущем шаге нашего алгоритма она называлась
вершин, и процесс завершился. Если осталась одна вершина, то на предыдущем шаге нашего алгоритма она называлась 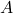 и была соединена с вершиной
и была соединена с вершиной 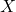 или
или 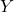 , которую объявили стратегически значимой, значит, для нее условие выполнено, и стратегически значимыми было объявлено не более
, которую объявили стратегически значимой, значит, для нее условие выполнено, и стратегически значимыми было объявлено не более ![Rendered by QuickLaTeX.com [2 \cdot 2016 / 3]=1344](https://mathgraphs.ru/wp-content/ql-cache/quicklatex.com-1c43dcabee4c4dc839fd00b382d026be_l3.png) вершин. Если же осталось две вершины, то, во-первых, они смежны, так как граф связности не теряет; во-вторых, одна из этих двух вершин была соединена с вершиной
вершин. Если же осталось две вершины, то, во-первых, они смежны, так как граф связности не теряет; во-вторых, одна из этих двух вершин была соединена с вершиной 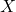 или
или 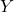 , объявленной стратегически значимой на предыдущем шаге. Поэтому достаточно объявить стратегически значимой лишь одну из этих двух вершин, чтобы условие выполнялось. Значит, и в этом случае стратегически значимыми будет объявлено не более
, объявленной стратегически значимой на предыдущем шаге. Поэтому достаточно объявить стратегически значимой лишь одну из этих двух вершин, чтобы условие выполнялось. Значит, и в этом случае стратегически значимыми будет объявлено не более ![Rendered by QuickLaTeX.com [2 \cdot 2015 / 3]+1=1344](https://mathgraphs.ru/wp-content/ql-cache/quicklatex.com-98a18af9b63870d7f48706f2eab3da24_l3.png) вершин.
вершин.
![]() из остальных 101. Докажите, что найдутся два кружковца, не входящих в эту десятку, таких, что каждый из десятки знает хотя бы одного из этих двоих.
из остальных 101. Докажите, что найдутся два кружковца, не входящих в эту десятку, таких, что каждый из десятки знает хотя бы одного из этих двоих.![]() пар дружков. Стало быть, вместе все 10 знатоков могут испортить максимум 1900 пар дружков, а всего пар дружков —
пар дружков. Стало быть, вместе все 10 знатоков могут испортить максимум 1900 пар дружков, а всего пар дружков — ![]() . Поэтому найдется неиспорченная пара дружков (и даже не меньше 3150 таких пар), что и требовалось доказать.
. Поэтому найдется неиспорченная пара дружков (и даже не меньше 3150 таких пар), что и требовалось доказать.