В стране из 1000 городов некоторые города соединены дорогами, по которым можно двигаться в обе стороны. Известно, что в этой стране нет циклического маршрута. При каком наибольшем 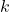 всегда можно выбрать
всегда можно выбрать 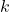 городов так, чтобы каждый выбранный город был соединен не более чем с двумя из остальных выбранных?
городов так, чтобы каждый выбранный город был соединен не более чем с двумя из остальных выбранных?
Подсказка
Назовем пауком город, соединенный ровно с тремя другими, попарно не соединенными дорогами. Рассмотрим 250 пауков (всего 1000 городов). Если 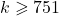 , то в одном из пауков выбраны все 4 города, что противоречит условию.
, то в одном из пауков выбраны все 4 города, что противоречит условию.
Решение
Ответ. 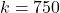 . Решение. Пример. Назовем пауком город, соединенный ровно с тремя другими, попарно не соединенными дорогами. Рассмотрим 250 пауков (всего 1000 городов). Если
. Решение. Пример. Назовем пауком город, соединенный ровно с тремя другими, попарно не соединенными дорогами. Рассмотрим 250 пауков (всего 1000 городов). Если 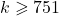 , то в одном из пауков выбраны все 4 города, что противоречит условию.
, то в одном из пауков выбраны все 4 города, что противоречит условию.
Оценка. Рассмотрим граф: вершины — города, рёбра — дороги. Если граф не связный, будем проводить по ребру между компонентами связности, пока он не станет связным. Ясно, что такая процедура не увеличит искомое число 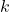 и не добавит в граф циклы.
и не добавит в граф циклы.
Итак, мы можем считать, что рассматриваемый граф — дерево. Индукцией по 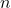 докажем, что в дереве на
докажем, что в дереве на 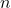 вершинах можно выбрать
вершинах можно выбрать 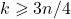 вершин так, чтобы выполнялось условие задачи. Такое множество вершин будем называть хорошим.
вершин так, чтобы выполнялось условие задачи. Такое множество вершин будем называть хорошим.
База: 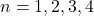 очевидна.
очевидна.
Переход: от всех меньших 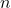 к
к 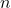 . Подвесим дерево за вершину и рассмотрим вершину
. Подвесим дерево за вершину и рассмотрим вершину  самого нижнего уровня. Если у ее предка
самого нижнего уровня. Если у ее предка 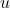 не менее трёх потомков, то выкинем
не менее трёх потомков, то выкинем 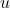 и всех ее потомков.
и всех ее потомков.
В оставшемся дереве выберем хорошее множество и добавим всех потомков 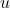 . Полученное множество будет хорошим для исходного дерева, и в нём не менее
. Полученное множество будет хорошим для исходного дерева, и в нём не менее 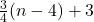 вершины.
вершины.
Если у вершины 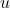 ровно 2 потомка
ровно 2 потомка  и
и 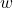 , то рассмотрим её предка
, то рассмотрим её предка 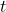 . Выкинем вершины
. Выкинем вершины 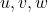 и
и 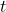 и, если понадобится, добавим рёбра для того, чтобы получилось дерево. В получившемся дереве выберем хорошее множество из не менее
и, если понадобится, добавим рёбра для того, чтобы получилось дерево. В получившемся дереве выберем хорошее множество из не менее 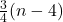 вершин, после чего добавим к нему вершины
вершин, после чего добавим к нему вершины 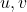 и
и 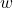 .
.
Итак, мы можем считать, что у любой вершины с нижнего уровня предок имеет степень ровно 2. Пусть  — вершина нижнего уровня,
— вершина нижнего уровня, 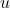 — её предок,
— её предок, 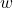 — предок
— предок 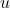 . У всех потомков (не обязательно прямых)
. У всех потомков (не обязательно прямых) 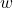 степень 1 или 2 . Если у
степень 1 или 2 . Если у 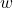 всего
всего 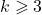 потомков (не обязательно прямых). Выкинем
потомков (не обязательно прямых). Выкинем 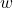 и всех её (не обязательно прямых) потомков. В оставшемся графе хорошее множество содержит не менее
и всех её (не обязательно прямых) потомков. В оставшемся графе хорошее множество содержит не менее 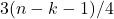 вершин. Добавим к ним всех
вершин. Добавим к ним всех 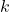 потомков
потомков 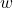 . Получим хорошее множество из не менее
. Получим хорошее множество из не менее 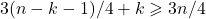 вершин в исходном дереве.
вершин в исходном дереве.
Наконец, если 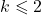 , то единственные потомки
, то единственные потомки 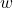 — это
— это 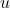 и
и  . Пусть
. Пусть 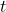 — предок
— предок 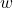 . Выкинем вершины
. Выкинем вершины 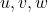 и
и 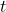 . В получившемся графе выберем хорошее множество из не менее
. В получившемся графе выберем хорошее множество из не менее 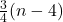 вершин, после чего добавим к нему вершины
вершин, после чего добавим к нему вершины 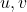 и
и 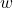 .
.