6 класс

Обозначьте число городов в республике за х.

Ответ: 67.

Решение: Пусть в отделившейся республике городов. Тогда количество дорог, соединяющих ее города, равно (из каждого из городов выходит по дороге, и каждая дорога при этом считается дважды), а количество дорог, ведущих из республики в остальные города страны, равно . По условию . Сократив на и решив получившееся уравнение, находим ответ.

Постройте пример. Поставьте детей по кругу.

Ответ: Нет.

Решение: Построим пример. Выстроим учеников по кругу, и пусть каждый пошлёт подарки 9 следующим по часовой стрелке. Возьмём любых троих и рассмотрим три десятки учеников каждая из которых состоит из одного из трёх взятых и девятерых, которым он послал подарки. Если никто из этих троих не посылал никому подарка, то три этих десятки учеников не должны пересекаться. Но тогда в классе не меньше 30 учеников, а по условию их там 29.

Разделите числа на 10 групп.

Разобьём числа на десять десятков: , и числа из одного десятка будем соединять синей стрелкой, а из разных десятков — красной. Понятно, что по синим стрелкам мы не выйдем за пределы десятка, и потому пройдем не больше 9 стрелок, а идя по красным стрелкам, мы каждый раз будем попадать в новый десяток и также пройдем не больше 9 стрелок.

Сколько боёв было сыграно в любой из школ?

Каждая команда сыграла в чемпионате 15 боев. Чтобы поиграть во всех школах, кроме своей, она должна была сыграть в каждой из них по одному разу. Но это значит, что в любой данной школе за время чемпионата должны были сыграть по одному разу 15 команд (все, кроме своей). Но в каждом бое участвуют две команды, поэтому общее число команд, игравших в данной школе, должно быть чётным. Полученное противоречие показывает, что так, как сказано в условии задачи, случиться не могло.

Для каждой комиссии создайте антикомиссию из всех не входящих в эту комиссию депутатов.

Ответ: 9.

Решение: Для каждой комиссии создадим антикомиссию из всех не входящих в эту комиссию депутатов. В каждой антикомиссии не меньше 11 депутатов, и разные антикомиссии не пересекаются (иначе в две соответствующие комиссии входили бы не все депутаты). Поэтому антикомиссий, а, стало быть, и комиссий не больше 9. Пример на 9: нумеруем депутатов числами от 1 до 100, и в -ую комиссию включаем всех, чей номер при делении на 9 даёт остаток, не равный .

Пусть первую республику со второй соединяют дорог. Тогда сколько дорог внутри республик?

Пусть первую республику со второй соединяют дорог. Тогда сумма количеств дорог, выходящих из городов первой республики, равна , и всего внутренних дорог в первой республике окажется ( ) , так как каждая из них учтена дважды. Аналогично показываем, что во второй республике также ( ) 2 внутренних дорог.

Отметим мальчиков синими точками, девочек — красными, а тех, кто танцевал друг с другом, соединим линиями. По условию из всех синих точек выходит поровну линий, и потому общее число линий делится на 30 .

Отметим мальчиков синими точками, девочек — красными, а тех, кто танцевал друг с другом, соединим линиями. По условию из всех синих точек выходит поровну линий, и потому общее число линий делится на 30 . Из красных точек может выходить линий. Заметим, что . Чтобы не нашлось двух девочек, танцевавших с одним и тем же количеством юношей, надо вычесть из этой суммы число от 0 до 30 так, чтобы разность разделилась на 30 . Но единственное подходящее для этого число 15 по условию вычесть нельзя.

Предположим, что нашлись пять человек, которые имеют не более пяти общих знакомых. Рассмотрим десятку, содержащую этих пятерых человек и всех их общих знакомых.

Предположим, что нашлись пять человек, которые имеют не более пяти общих знакомых. Рассмотрим десятку, содержащую этих пятерых человек и всех их общих знакомых. По условию выбранные 10 человек имеют общего знакомого, но тогда мы нашли ещё одного общего знакомого для пятерых человек. Противоречие.

Цикл длины 4 можно получить, только соединив концы цепи длины 3. Поэтому тот, после хода которого образуется цепь длины 3, проиграл.

Ответ. Вася.

Решение. Цикл длины 4 можно получить, только соединив концы цепи длины 3. Поэтому тот, после хода которого образуется цепь длины 3, проиграл. Значит, концы цепи длины 2 соединять с другими точками нельзя. Стратегия Васи: после каждого хода Пети соединять ту же красную точку с какой-то синей, которая ещё не соединена ни с какой другой. Тогда после каждой пары ходов Пети и Васи число не соединённых с другими синих точек будет уменьшаться на 2 , и после 50 -го хода Васи каждая синяя точка будет концом цепи длины 2. Своим 51-м ходом Петя создаст цепь длины 3 и проиграет.

Пример. Пусть в группе 20 девочек и 20 мальчиков. Все девочки знакомы со всеми мальчиками, но никакие девочки не знакомы друг с другом и никакие мальчики не знакомы друг с другом. Легко видеть, что такая группа удовлетворяет условию.

Ответ: 40 школьников.

Решение. Пример. Пусть в группе 20 девочек и 20 мальчиков. Все девочки знакомы со всеми мальчиками, но никакие девочки не знакомы друг с другом и никакие мальчики не знакомы друг с другом. Легко видеть, что такая группа удовлетворяет условию.

Оценка. Предположим, что у какого-то школьника есть хотя бы 21 знакомый 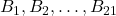. По условию, все его знакомые незнакомы. Но тогда у школьника 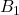есть 20 незнакомых и они незнакомы друг с другом. Противоречие. Следовательно, у каждого школьника не более 20 знакомых и, аналогично, не более 20 незнакомых. Тогда школьников всего не более 41. Осталось доказать, что невозможен случай, когда школьников ровно 41 . Пусть так. Тогда у школьника ровно 20 знакомых и ровно 20 незнакомых . Причем все 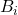попарно незнакомы, а все попарно знакомы. У 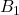также должно быть ровно 20 знакомых, которые незнакомы между собой. Он уже знает и не знает никого из . 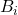Следовательно, он знаком с хотя бы 19 школьниками из . Но попарно знакомы. Противоречие.