Уральский Турнир Юных Математиков — Страница 2 — Задачи на Графы

Задача 015

01.01.2025 от

В классе 29 детей. Каждый из детей послал новогодние подарки 9 своим одноклассникам. Всегда ли найдутся трое детей, ни один из которых не посылал подарки никому из двух других?

Подсказка

Постройте пример. Поставьте детей по кругу.

Решение

Ответ: Нет.

Решение: Построим пример. Выстроим учеников по кругу, и пусть каждый пошлёт подарки 9 следующим по часовой стрелке. Возьмём любых троих и рассмотрим три десятки учеников каждая из которых состоит из одного из трёх взятых и девятерых, которым он послал подарки. Если никто из этих троих не посылал никому подарка, то три этих десятки учеников не должны пересекаться. Но тогда в классе не меньше 30 учеников, а по условию их там 29.

Задача 016

01.01.2025 от

Любые два натуральных числа от 1 до 100 включительно соединены стрелкой, ведущей от меньшего числа к большему. Как раскрасить эти стрелки в красный и синий цвета так, чтобы любой одноцветный путь проходил не более, чем по девяти стрелкам?

Подсказка

Разделите числа на 10 групп.

Решение

Разобьём числа на десять десятков: $1-10,11-20, \ldots, 91-100$ , и числа из одного десятка будем соединять синей стрелкой, а из разных десятков — красной. Понятно, что по синим стрелкам мы не выйдем за пределы десятка, и потому пройдем не больше 9 стрелок, а идя по красным стрелкам, мы каждый раз будем попадать в новый десяток и также пройдем не больше 9 стрелок.

Задача 018

01.01.2025 от

На танцах было 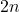$2 n$ мальчиков и 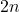$2 n$ девочек. Боря танцевал со всеми девочками, Аня танцевала со всеми мальчиками, и для любых двух девочек есть ровно n мальчиков, танцевавших ровно с одной из них. Докажите, что каждый мальчик, кроме Бори, танцевал ровно с 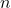$n$ девочками.

Подсказка

Рассмотрите вместе с Аней ещё одну (любую) девочку. Что следует их условия?

Решение

Возьмём Аню и любую другую девочку Д. По условию, ровно с одной девочкой из этих двух танцевало ровно 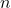$n$ мальчиков. Так как с Аней танцевали все мальчики, то эти 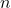$n$ мальчиков танцевали именно с ней, а остальные 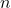$n$ мальчиков танцевали и с ней, и с Д. Итак, с каждой девочкой, кроме Ани, танцевали ровно 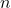$n$ мальчиков. Возьмём любых двух таких девочек. Пусть с обеими танцевали 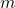$m$ мальчиков. Тогда ровно с одной танцевали 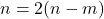$n=2(n-m)$ мальчиков, откуда $m=n / 2$ .

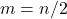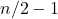Забудем про Аню и Борю. Тогда каждая из девочек танцевала с $n-1$ мальчиком, а с каждыми двумя девочками танцевали $n / 2-1$ мальчиков. Занумеруем мальчиков и пусть 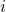$i$ -ый мальчик танцевал с 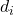$d_{i}$ девочками. Тогда троек, состоящих из мальчика и двух девочек, с которыми он танцевал, будет 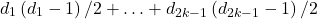$d_{1}\left(d_{1}-1\right) / 2+\ldots+d_{2 k-1}\left(d_{2 k-1}-1\right) / 2$ . С другой стороны, число таких троек равно 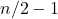$n / 2-1$ , умноженному на количество пар девочек, то есть $(n / 2-1)(2 n-1)(n-1)$ .
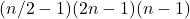Заметим, что

$d_{1}\left(d_{1}-1\right) / 2+\ldots+d_{2 k-1}\left(d_{2 k-1}-1\right) / 2=\left(d_{1}^{2}+\ldots+d_{2 n-1}^{2}\right) / 2-\left(d_{1}+\ldots+d_{2 n-1}\right) / 2 \text {. }$

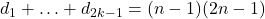Так как $d_{1}+\ldots+d_{2 k-1}=(n-1)(2 n-1)$ (считаем ту же сумму «со стороны девочек»), то получаем, что

$d_{1}^{2}+\ldots+d_{2 n-1}^{2}=2(n / 2-1)(2 n-1)(n-1)+(n-1)(2 n-1)=(n-1)^{2}(2 n-1) .$

С другой стороны, по неравенству между средним арифметическим и средним квадратическим

$d_{1}^{2}+\ldots+d_{2 n-1}^{2} \geq\left(d_{1}+\ldots+d_{2 n-1}\right)^{2} /(2 n-1)=(n-1)^{2}(2 n-1)$

причём равенство достигается только при 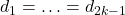$d_{1}=\ldots=d_{2 k-1}$ . Итак, все 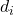$d_{i}$ равны между собой, откуда 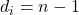$d_{i}=n-1$ , что и (вспомним про Аню!) требовалось доказать.

Задача 021

01.01.2025 от

В компании из 300 человек каждый знаком ровно с тремя другими. При каком наименьшем $k$ про такую компанию можно наверняка утверждать, что среди любых $k$ человек найдутся двое знакомых?

Подсказка

Попробуйте для начала подумать над компанией из 150 человек.

Решение

Ответ: 151.
Решение: Допустим, удалось выбрать 151 человека, не знакомых друг с другом. У них вместе 453 знакомства с оставшимися 149 людьми, но у тех вместе всего 447 знакомств — противоречие. Таким образом, среди любых 151 человека найдутся двое знакомых. Покажем, что 150 человек, не знакомых друг с другом, могут найтись. Разобьём компанию на 50 шестёрок, каждую шестёрку — на две тройки, и пусть в каждой шестёрке каждый человек из одной тройки знаком с каждым человеком из другой; в набор из 150 человек возьмём по одной тройке из каждой шестёрки.

Задача 023

01.01.2025 от

В однокруговом чемпионате по матбоям участвовали 16 команд из 16 разных школ. Каждый бой проходил в одной из школ-участниц. Могло ли по окончании чемпионата случиться, что каждая команда сыграла во всех школах, кроме своей?

Подсказка

Сколько боёв было сыграно в любой из школ?

Решение

Каждая команда сыграла в чемпионате 15 боев. Чтобы поиграть во всех школах, кроме своей, она должна была сыграть в каждой из них по одному разу. Но это значит, что в любой данной школе за время чемпионата должны были сыграть по одному разу 15 команд (все, кроме своей). Но в каждом бое участвуют две команды, поэтому общее число команд, игравших в данной школе, должно быть чётным. Полученное противоречие показывает, что так, как сказано в условии задачи, случиться не могло.

Задача 025

01.01.2025 от

2016 мальчиков выбирают девочек. Каждый мальчик выбирает ровно двух девочек: одну блондинку и одну брюнетку. Оказалось, что для любого натурального числа $k, 1 \leq k \leq 80$ , найдется девочка (блондинка или брюнетка), которую выбрали ровно $k$ мальчиков. Докажите, что какие-то два мальчика выбрали одних и тех же девочек.

Подсказка

Зафиксируйте 80 вершин со степенями $1,2, \ldots, 80$ соответственно.

Решение

Рассмотрим двудольный (мульти)граф, где вершины — блондинки и брюнетки, а рёбра — выборы мальчиков. В нем 2016 рёбер. Надо доказать, что есть два ребра с общими концами.

Зафиксируем 80 вершин со степенями $1,2, \ldots, 80$ соответственно; назовём их выбранными. Пусть имеется $k$ рёбер, оба конца которых выбраны; также назовём их выбранными. Тогда рёбер, один конец которых выбран, будет $1+2+\ldots+80-2 k$ . С другой стороны, их не больше, чем 2016- $k$ , откуда $k \geq 1+2+\ldots+80-2016=1224$ .

Рассмотрим выбранные вершины со степенями $1,2, \ldots, 26$ . Из них исходит не более $1+2+\ldots+26=351$ выбранного ребра. Значит, остальные 54 вершины связывают не менее $1224-351=873$ рёбер. С другой стороны, пусть среди этих 54 вершин $x$ блондинок и $54-x$ брюнеток, и между любыми двумя вершинами — не более одного ребра. Тогда всего между этими вершинами не более $x(54-x) \leq(x+54-x)^{2} / 2^{2}=27^{2}=729$ рёбер. Противоречие.

Задача 026

01.01.2025 от

В городе 2015 жителей, которые организовали $n$ клубов. Оказалось, что для каждых двух клубов количество жителей, состоящих хотя бы в одном из них, не больше 2011. Однако для любых трёх клубов хотя бы в одном из них состоит каждый житель города. Найдите наибольшее возможное значение $n$ .

Подсказка

По первому условию для каждых двух клубов $A$ и $B$ найдутся 4 человека, которые в этих клубах не состоят. Но по второму условию эти 4 человека состоят во всех оставшихся клубах.

Решение

Ответ: 32.

Решение: Оценка. По первому условию для каждых двух клубов $A$ и $B$ найдутся 4 человека, которые в этих клубах не состоят. Но по второму условию эти 4 человека состоят во всех оставшихся клубах. Отсюда следует, что четверки, соответствующие разным парам клубов, не пересекаются. Отсюда $4 C_{n}^{2}<2015$ , то есть $n \leq 32$ . Пример. Выделим среди жителей города $C_{32}^{2}=496$ непересекающихся четверок. Каждой из них поставим в соответствие пару клубов, в которых жители, входящие в неё, они не состоят, так, чтобы каждой паре клубов соответствовала какая-то четверка. Остальные (не входящие в четверки) жители состоят во всех клубах.

Задача 027

01.01.2025 от

В кружке занимаются $2 n$ человек. Кружок называется однородным, если у каждого кружковца одно и то же количество друзей в кружке. Докажите, что кружок однороден тогда и только тогда, когда при любом его разбиении на две команды по $n$ учеников количества пар друзей в командах равны.

Подсказка

Разделите вершины на две равные группы $A$ и $B$ .

Решение

Рассмотрим граф знакомств. Разделим вершины на две равные группы $A$ и $B$ . Пусть $S_{A}\left(S_{B}\right)$ — сумма степеней вершин, входящих в $A(B)$ , а $R$ — количество знакомств между учениками из $A$ и $B$ . Тогда количество знакомств $N_{A}$ внутри $A$ равно $\left(S_{A}-R\right) / 2$ . 1) Пусть у всех одинаковое число друзей. Тогда при разбиении на равные группы $A$ и $B, S_{A}=S_{B}$ , следовательно, $N_{A}=N_{B}$ . 2) Пусть не у всех одинаковое число друзей. Составим $A$ из $n$ вершин с наименьшими степенями. Тогда $S_{A}<S_{B}$ , и, следовательно, $N_{A}<N_{B}$ .

Задача 028

01.01.2025 от

В стране 300 городов. Некоторые пары городов соединены дорогами. Оказалось, что из каждого города выходит ровно 10 дорог. Страна распалась на две республики Иксия и Игрекия. В Иксии оказалось 200 городов, а в Игрекии — 100 городов. Оказалось, что число дорог, соединяющих города Иксии, равно $x$ , а дорог, соединяющих города Игрекии, равно $y$ . Чему может быть равно $x-y$ ?

Подсказка

Пусть из Иксии в Игрекию ведёт $z$ дорог. Сколько ещё дорог в республиках?

Решение

Ответ. 500. Решение. Пусть из Иксии в Игрекию ведёт $z$ дорог. Тогда из городов Иксии в совокупности выходит $10 \cdot 200=2 x+z$ дорог, а из городов Игрекии — $10 \cdot 100=2 y+z$ дорог ( $x$ и $y$ умножаются на 2 , так как каждая дорога, соединяющая города одной республики, считается тут дважды). Вычитая два полученных равенства и деля результат пополам, получаем ответ.

Задача 029

01.01.2025 от

В парламенте Анчурии заседает 100 депутатов. Они организовали несколько комиссий. Оказалось, что в каждой комиссии менее 90 депутатов. Кроме того, если рассмотреть любые две комиссии, то каждый депутат войдёт хотя бы в одну из них. Какое наибольшее количество комиссий могло быть создано?

Подсказка

Для каждой комиссии создайте антикомиссию из всех не входящих в эту комиссию депутатов.

Решение

Ответ: 9.

Решение: Для каждой комиссии создадим антикомиссию из всех не входящих в эту комиссию депутатов. В каждой антикомиссии не меньше 11 депутатов, и разные антикомиссии не пересекаются (иначе в две соответствующие комиссии входили бы не все депутаты). Поэтому антикомиссий, а, стало быть, и комиссий не больше 9. Пример на 9: нумеруем депутатов числами от 1 до 100, и в $k$ -ую комиссию включаем всех, чей номер при делении на 9 даёт остаток, не равный $k-1(k=1,2, \ldots, 9)$ .