Прямоугольник разбит на 2016 прямоугольничков со сторонами, параллельными его сторонам. Узел — это вершины этих прямоугольничков. Отрезок, лежащий на стороне некоторого прямоугольничка, назовём базисным, если его концы являются узлами и на нем нет других узлов. Какое наименьшее количество базисных отрезков может получиться при разбиении прямоугольника?
Подсказка
Обозначьте узлы за вершины, а базисные отрезки за рёбра. Посчитайте наименьшее количество вершин степени 3.
Решение
Ответ: 4122.
Решение: Рассмотрим граф, вершинами которого являются узлы, а рёбрами — базисные отрезки. Пусть в этом графе 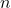 вершин степени
вершин степени 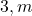 вершин степени 4 ; также в нём имеется четыре вершины степени 2.
вершин степени 4 ; также в нём имеется четыре вершины степени 2.
Посчитаем сумму углов всех прямоугольников. С одной стороны, она равняется 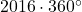 . С другой стороны, вершина степени 2 вносит в эту сумму
. С другой стороны, вершина степени 2 вносит в эту сумму 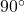 , вершина степени 3 —
, вершина степени 3 — 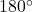 , вершина степени
, вершина степени 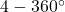 . Следовательно,
. Следовательно, 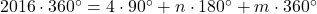 , т.е.
, т.е. 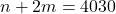 . Пусть количество рёбер в нашем графе равняется
. Пусть количество рёбер в нашем графе равняется  . Тогда
. Тогда 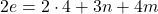 . Подставляя
. Подставляя 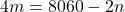 , имеем
, имеем 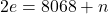 . Таким образом, нам нужно доказать, что наименьшее значение, которое может принимать
. Таким образом, нам нужно доказать, что наименьшее значение, которое может принимать 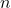 , равняется 176.
, равняется 176.
Для начала докажем, что 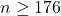 . Проведём через все стороны прямоугольников, не лежащие на сторонах квадрата, прямые. Возьмём какую-нибудь прямую и посмотрим на крайние узлы, оказавшиеся на ней. Соответствующие им вершины, очевидно, не могут иметь степени 2 и 4; значит, они имеют степень 3. Также, очевидно, что никакие две из рассматриваемых вершин не могут совпасть. Следовательно, если
. Проведём через все стороны прямоугольников, не лежащие на сторонах квадрата, прямые. Возьмём какую-нибудь прямую и посмотрим на крайние узлы, оказавшиеся на ней. Соответствующие им вершины, очевидно, не могут иметь степени 2 и 4; значит, они имеют степень 3. Также, очевидно, что никакие две из рассматриваемых вершин не могут совпасть. Следовательно, если  и
и 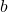 — количество вертикальных и горизонтальных прямых соответственно, то вершин степени 3 хотя бы
— количество вертикальных и горизонтальных прямых соответственно, то вершин степени 3 хотя бы 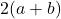 . С другой стороны, эти прямые разбивают квадрат на
. С другой стороны, эти прямые разбивают квадрат на 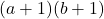 прямоугольничков, из которых складываются 2016 прямоугольников из условия. Значит,
прямоугольничков, из которых складываются 2016 прямоугольников из условия. Значит, 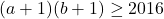 . Следовательно,
. Следовательно, 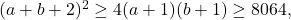 откуда
откуда 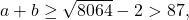 а
а 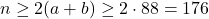 , что и требовалось.
, что и требовалось.
Теперь приведём пример, в котором 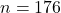 . Разделим большой квадрат 44 вертикальными и 44 горизонтальными прямыми на
. Разделим большой квадрат 44 вертикальными и 44 горизонтальными прямыми на 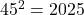 маленьких квадратиков. Далее сотрём 9 базисных отрезков, примыкающих к одной из сторон большого квадрата. Тогда прямоугольников разбиения получится ровно 2016, а на каждой из 88 проведённых прямых будет ровно по 2 узла, из которых выходит по 3 базисных отрезка, что и требовалось.
маленьких квадратиков. Далее сотрём 9 базисных отрезков, примыкающих к одной из сторон большого квадрата. Тогда прямоугольников разбиения получится ровно 2016, а на каждой из 88 проведённых прямых будет ровно по 2 узла, из которых выходит по 3 базисных отрезка, что и требовалось.
![]() городов, каждые два из которых соединены прямым автобусным сообщением в обе стороны. Сколькими способами можно попасть из города
городов, каждые два из которых соединены прямым автобусным сообщением в обе стороны. Сколькими способами можно попасть из города ![]() в другой город
в другой город ![]() , проехав на автобусе ровно
, проехав на автобусе ровно ![]() раз? Маршрут может проходить через любой город (в том числе
раз? Маршрут может проходить через любой город (в том числе ![]() и
и ![]() ), а также использовать любой рейс между городами более одного раза.
), а также использовать любой рейс между городами более одного раза.![]() .
.![]() количество маршрутов длины
количество маршрутов длины ![]() из
из ![]() в
в ![]() . Выедем из города
. Выедем из города ![]() и будем ехать каждый раз в произвольный город. На каждом шаге у нас будет ровно
и будем ехать каждый раз в произвольный город. На каждом шаге у нас будет ровно ![]() вариант, поэтому всего маршрутов длины
вариант, поэтому всего маршрутов длины ![]() выходящих из
выходящих из ![]() , будет ровно
, будет ровно ![]() . Заметим, что каждый такой маршрут либо заканчивается в городе
. Заметим, что каждый такой маршрут либо заканчивается в городе ![]() , либо можно сделать еще один ход в
, либо можно сделать еще один ход в ![]() . Поэтому
. Поэтому ![]() . Теперь искомую формулу можно доказать методом математической индукции: базой является
. Теперь искомую формулу можно доказать методом математической индукции: базой является ![]() , а переход следует из формулы (*).
, а переход следует из формулы (*).