B стране 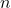 городов, один из которых является столицей. Между некоторыми парами городов налажено авиасообщение. Расстоянием между городами называется минимальное количество перелетов, которые необходимо совершить, чтобы добраться от одного города до другого. Правительство хочет закрыть авиасообщение между некоторыми парами городов, но чтобы расстояние от столицы до любого другого города не изменилось. Известно, что существует нечетное количество способов, которыми правительство может это сделать. В том числе считается способ, в котором не закрывается ничего.
городов, один из которых является столицей. Между некоторыми парами городов налажено авиасообщение. Расстоянием между городами называется минимальное количество перелетов, которые необходимо совершить, чтобы добраться от одного города до другого. Правительство хочет закрыть авиасообщение между некоторыми парами городов, но чтобы расстояние от столицы до любого другого города не изменилось. Известно, что существует нечетное количество способов, которыми правительство может это сделать. В том числе считается способ, в котором не закрывается ничего.
Докажите, что нельзя, стартовав в некотором городе и совершив нечетное число перелетов, вернуться обратно в него.
Подсказка
Подвесим граф за вершину-столицу С. Вспомним, что вершины 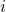 -го яруса определяются в точности как те вершины, расстояние от которых до C равно
-го яруса определяются в точности как те вершины, расстояние от которых до C равно 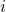 .
.
Решение
Введём граф, в котором вершины — города, рёбра — наличие авиасообщения. Подвесим граф за вершину-столицу С. Вспомним, что вершины 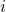 -го яруса определяются в точности как те вершины, расстояние от которых до C равно
-го яруса определяются в точности как те вершины, расстояние от которых до C равно 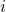 . В таком графе рёбра могут быть либо внутри одного яруса, либо между ярусами с номерами, отличающимися на 1. Мы рассматриваем множества ребер, при удалении которых сохраняется ярус каждой вершины в нашем графе, будем называть их интересными. Если некоторое ребро
. В таком графе рёбра могут быть либо внутри одного яруса, либо между ярусами с номерами, отличающимися на 1. Мы рассматриваем множества ребер, при удалении которых сохраняется ярус каждой вершины в нашем графе, будем называть их интересными. Если некоторое ребро  соединяет две вершины одного яруса, то при включении или исключении
соединяет две вершины одного яруса, то при включении или исключении  интересность множества ребер не меняется. Таким образом, все интересные множества разбиваются на пары, что противоречит условию. Следовательно, в графе нет ребер, соединяющих вершины одного яруса. Тогда в любом цикле ярусы соседних вершин отличаются на 1 , тем самым они имеют разную четность. Значит, любой цикл в данном графе имеет четную длину, что и требовалось.
интересность множества ребер не меняется. Таким образом, все интересные множества разбиваются на пары, что противоречит условию. Следовательно, в графе нет ребер, соединяющих вершины одного яруса. Тогда в любом цикле ярусы соседних вершин отличаются на 1 , тем самым они имеют разную четность. Значит, любой цикл в данном графе имеет четную длину, что и требовалось.
![]() -ую комиссию включаем всех, чей номер при делении на 9 даёт остаток, не равный
-ую комиссию включаем всех, чей номер при делении на 9 даёт остаток, не равный ![]() .
.