В парламенте 2008 депутатов, разбитых на 3 фракции. Назовем депутата единолюбом, если все его друзья из одной фракции. Докажите, что найдется депутат, который может перейти в другую фракцию, и при этом не появится новых единолюбов.
Подсказка
Допустим, утверждение задачи неверно для какого-либо графа на 2008 вершинах. Будем говорить, что вершина 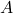 портит вершину
портит вершину 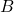 , если вершину
, если вершину 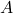 можно перекрасить так, чтобы вершина
можно перекрасить так, чтобы вершина 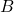 , которая не была плохой, стала плохой. Заметим, что если степень вершины не равна 2 , её можно испортить не более чем одним способом.
, которая не была плохой, стала плохой. Заметим, что если степень вершины не равна 2 , её можно испортить не более чем одним способом.
Решение
Сформулируем задачу на языке графов и заменим разбиение на фракции раскраской вершин графа на три цвета, а депутата-единолюба на плохую вершину.
Допустим, утверждение задачи неверно для какого-либо графа на 2008 вершинах. Будем говорить, что вершина 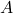 портит вершину
портит вершину 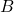 , если вершину
, если вершину 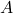 можно перекрасить так, чтобы вершина
можно перекрасить так, чтобы вершина 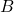 , которая не была плохой, стала плохой.
, которая не была плохой, стала плохой.
Заметим, что если степень вершины не равна 2 , её можно испортить не более чем одним способом. В самом деле, вершины степени 0 и 1 всегда плохие, поэтому испортить их вообще нельзя. Пусть степень вершины больше 2. Если её можно испортить, то все соседние вершины, кроме одной, покрашены в один цвет, а одна — в другой, и этот цвет, как и вершина, которую надо в него перекрашивать, определены однозначно. Вершину же степени 2 можно, очевидно, испортить не более чем двумя способами.
Каждую вершину можно перекрасить двумя способами. Поэтому количество способов, которыми можно испортить вершины нашего графа, равно 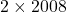 . С другой стороны, столько же должно получиться, если просуммировать по всем вершинам количество способов, которыми они могут быть испорчены. Поскольку в этой сумме все слагаемые не больше 2 , все они должны равняться 2. Это возможно только если в нашем графе степень каждой вершины равна 2 . Стало быть, он распадается на непересекающиеся циклы, причём каждую вершину каждого цикла можно испортить двумя способами. Такое возможно только если каждая вершина и те вершины, что идут в цикле через одну от неё, покрашены в три разных цвета. Нетрудно показать, что длина цикла в этом случае должна делиться на 3 . Но 2008 на 3 не делится.
. С другой стороны, столько же должно получиться, если просуммировать по всем вершинам количество способов, которыми они могут быть испорчены. Поскольку в этой сумме все слагаемые не больше 2 , все они должны равняться 2. Это возможно только если в нашем графе степень каждой вершины равна 2 . Стало быть, он распадается на непересекающиеся циклы, причём каждую вершину каждого цикла можно испортить двумя способами. Такое возможно только если каждая вершина и те вершины, что идут в цикле через одну от неё, покрашены в три разных цвета. Нетрудно показать, что длина цикла в этом случае должна делиться на 3 . Но 2008 на 3 не делится.
![]() до
до ![]() проходит через
проходит через ![]() . Тогда, цикл
. Тогда, цикл ![]() требует не более
требует не более ![]() часов, так как переезд от
часов, так как переезд от ![]() к
к ![]() и все остальные переходы требуют не более 8 часов каждый.
и все остальные переходы требуют не более 8 часов каждый. ![]() дорогами, требующими 4 часов каждая. Остальные города либо связаны дорогами, либо нет, чтобы общее число дорог равнялось 1000. Все дороги между ними требуют 8 часов. Легко видеть, что оценка достигается.
дорогами, требующими 4 часов каждая. Остальные города либо связаны дорогами, либо нет, чтобы общее число дорог равнялось 1000. Все дороги между ними требуют 8 часов. Легко видеть, что оценка достигается.